First published Mar'24
How Secure Hash Algorithm (SHA) is secure in 1 direction
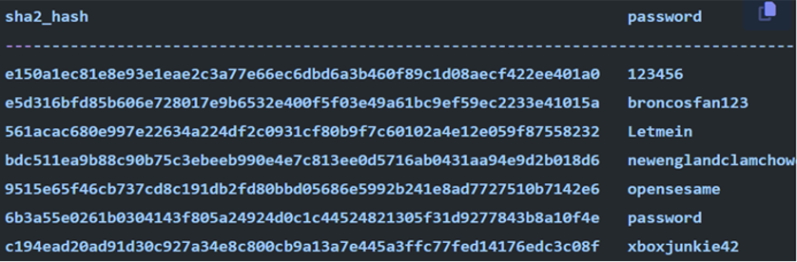
The SHA-256 algorithm produces a 256 bit result (a bit is a 0 or 1), an example is in the top picture. One way of cracking this is to use a massive look-up table (aka rainbow table) that maps all hash variations to a plain text – this is used a lot for the simpler passwords, see diagrams:
The bottom picture is an example of complexity v security – and already out of date so start using the longer ‘suggested passwords’ and change the key ones now!
Security increases logarithmically as it doubles (e.g. SHA-512), to keep ahead of using brute for from larger and larger computing power, especially if generative AI overcomes its massive maths blind spot. But this is diffused by a ‘salt’, i.e. simply a bunch of random characters that you prepend to the password before it is hashed. Luckily SQL and other main languages haven the SHA2(56) function

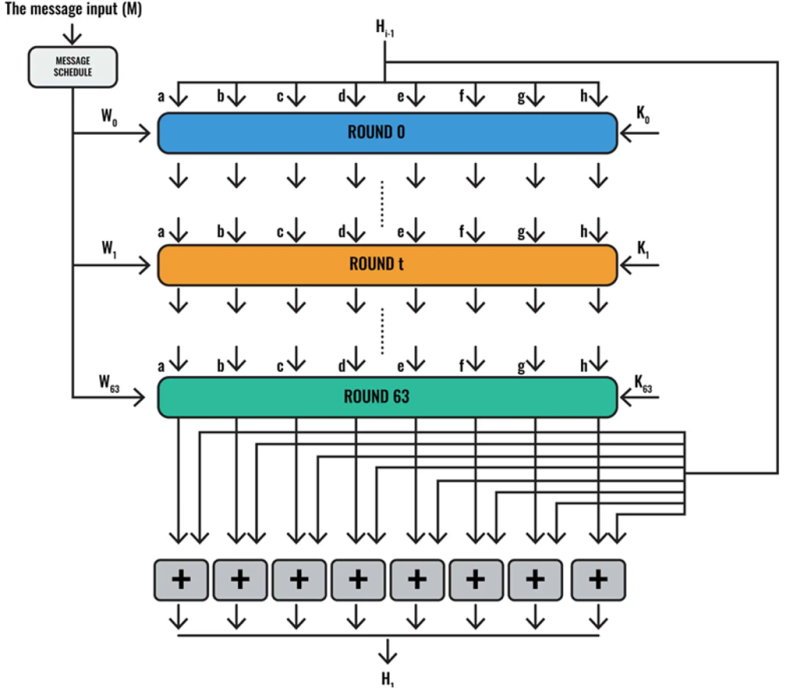
Algorithm Methodology
Full spec: https://nvlpubs.nist.gov/nistpubs/FIPS/NIST.FIPS.180-4.pdf
Usage: https://www.comparitech.com/blog/information-security/what-is-sha-2-algorithm/
The diagram that shows the 64 iterations of the SHA2(56) algorithm, SHA512 would have 80 rounds. Simple in one direction, and basically impossible in reverse. And the parts of this are:
o M - Input Message is padded out at the end to be a block of 512 bits
o W – the different rounds of the calculations:
> W (0-15)– The 512 bits are split up into 16 (0-15) blocks of 32-bits
> These are then all converted to hexadecimal to get away from the length of binary outputs
> W (16-64) – are created by using:
• W t = σ1 (Wt-2) + Wt-7 + σ0 (Wt-15) + Wt-16
• σ1(x) = ROTR17(x)⊕ROTR19(x)⊕SHR10(x)
• ROTR is the angular change in geometric algebra, which is the first part that makes it very hard to replicate in reverse
• ⊕ stands for XOR, which means that there are too many variants when being reversed engineers so would need a lot of power to break
• SHR shifts the bits to the left or right, so needs to know if using UTF-8 or UTF 16, usually the former in the web but new data systems need more efficiency so are moving to the latter. So SHR(x), moves the value to the left by x… scrambling the output more
• + is Modular addition. The + isn’t the usual, e.g. usually 76,487,639 + 98,094,034 = 174,581,673 but with modular addition the number is too long at 9 digits so the 1st number is thrown away so the answer is 74,581,673, another problem for reverse engineering
o H - This represents the working variables, which act as inputs in each round. There are eight of these variables, and they are updated at the end of each round. To begin, the initialization variables, H(0) are the hexadecimal form of the square roots of the first 8 prime number – that why prime numbers are of interest to all cryptographers as they obviously cannot be mistaken for another number. These don’t change and are: H(0)a = 6a09e667, H(0)b = bb67ae85, H(0)c = 3c6ef372, H(0)d = a54ff53a, H(0)e = 510e527f, H(0)f = 9b05688c, H(0)g = 1f83d9ab, H(0)h = 5be0cd19
o K (constant) – In each round the working variables are combined with round-appropriate value from the prior section. There are 64 separate 32-bit value for K, one for each round – these are the cube-root of the first 64 prime numbers. In SHA256 would be 32 bit each, and SHA512 is 80 bits, but here its easier to show then in hexadecimal: 428a2f98, 71374491, b5c0fbcf, e9b5dba5…
(if you've got this far you're my kind of person)
We need your consent to load the translations
We use a third-party service to translate the website content that may collect data about your activity. Please review the details in the privacy policy and accept the service to view the translations.
